前情提要

昨天大致上講解了 tokenizer 的部分，這是 LLM 的第一步，但現在這部分很方便直接套用就行。

0. 複習

在開始之前先複習一下高中數學，不管高中高職一定都學過"向量內積"，這裡借一下人家的圖片

1. 向量內積

   
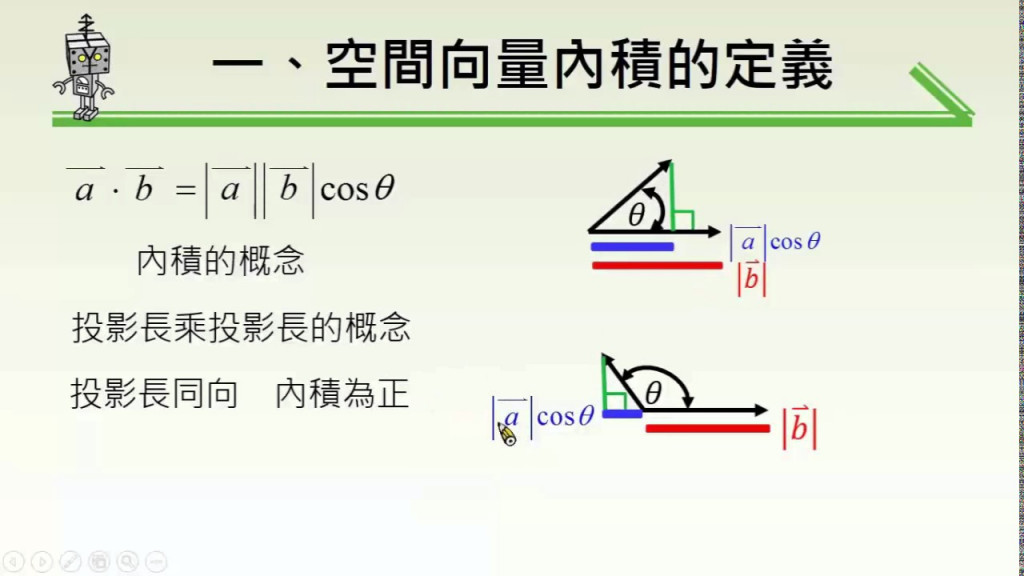
   向量內積 → 表示兩向量的夾角, 表示一個向量在另一個向量上的投影
   投影的值越大 → 兩個向量相關度高
   如果兩個向量夾角為九十度，那麼兩個向量線性無關

2. 加權平均

   接下來國中或高中在段考算平均的時候，會有加權平均，等下我們會用到分子的部分
   ex: (國文學分 x 國文分數 + 數學學分 x 數學分數 … ) / (總學分)

1. Embedding

參考文章: https://www.cnblogs.com/rossiXYZ/p/18741857 ，這個也是一系列的文章，寫得非常詳細非常不錯，我基本上都是在上面學習的，推薦給大家。
昨天我們已經學了 tokenizer 相關內容，不過後面其實還需要獨熱編碼(One-Hot Encoding), embedding 兩個部分。

• One-Hot Encoding: 假設四個字，就用四個位置來表示，一次只能有一個 1，依此類推
• embedding: 具備語意性的稠密多維度向量

以下表格是從上面文章當中圖做出來的，不過文章內的獨熱編碼有寫錯，所以這邊修正

我們先來一張圖更了解 embedding，文章舉例是一個數學家和物理學家，然後其中三個特徵，分別是: 可以跑, 喜歡咖啡, 專精物理，兩位學家都可以跑也都愛喝咖啡，所以兩者出來的分數會很接近，但最後一個特徵就差很多，那最後我想看整體的相似度，我們拿出高中學過的內積求 cos，越接近 1 代表越相似。

我們再用一個圖來了解怎麼從 index → one-hot → embedding (其實就是一個單層全連接而已)
  
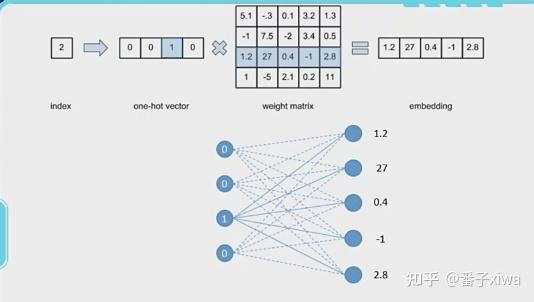
  圖片來源: https://zhuanlan.zhihu.com/p/492331266

一樣來幾個 QA

Question

1. 為什麼需要從 one-hot vector 轉成 embedding ??
2. 任何東西東可以轉換成 embedding ??

Answer

1. 維度太高：假設有 1,000 個詞，one-hot 向量就是 1,000 維，只有一個位置是 1，其餘全是 0 → 稀疏、浪費空間。
   沒有語意關係：one-hot 之間完全沒有距離概念，「貓」和「狗」的 one-hot 向量距離跟「貓」和「飛機」一樣。
   Embedding 優勢：可以把詞壓縮到一個固定低維度（例如 128 或 768），並且透過訓練讓相似的詞距離更近，保留語意關係。
2. 是的，幾乎所有都可以壓成 embedding，以下列出幾個 pretrained model
   文字: 最常見的 BERT
   聲音: 最常見的 wav2vec2.0, HuBERT, WavLM, NEST
   圖像: dino3

2. attention 觀念

核心觀念: 加權求和
文章參考: https://zhuanlan.zhihu.com/p/410776234 ，這篇我覺得是講的最好理解的，畢竟寫得比我好的一堆，底下只是整理成我能理解的。
底下的公式相信不陌生，基本上都有看過，但要看著公式就把程式寫出來需要花點心思了解觀念並動手實作。

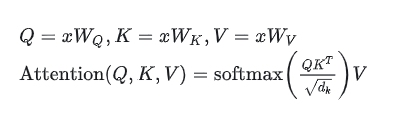
我們先把公式弱化成: softmax(XX^T)X，因為 Q, K, V 本質上都是由 x 轉換而來的
理解順序:
  
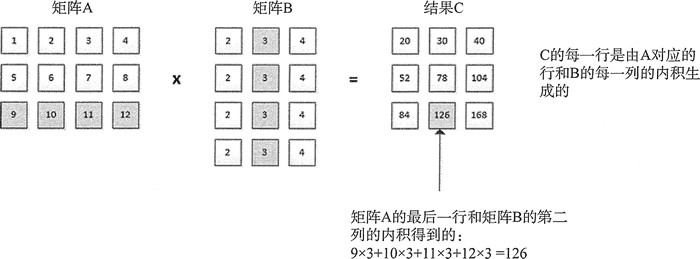
  圖片來源: C++ inner_product内积计算方法详解_c++ 内积-CSDN博客
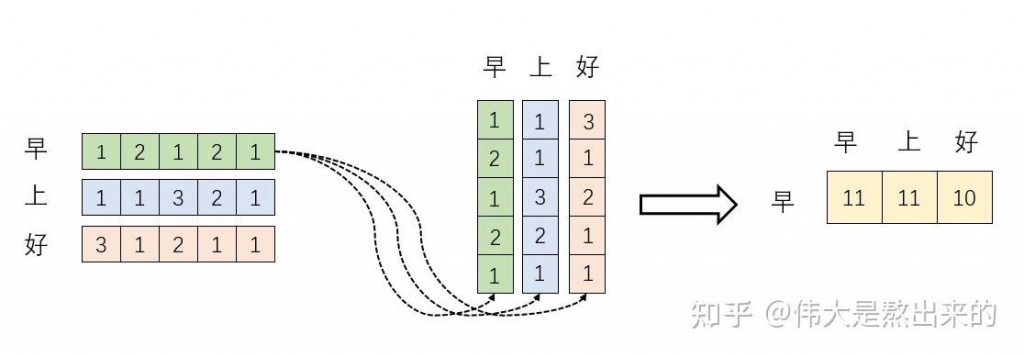
內積計算：XX^T

• X 每一行與轉置過後的 X 的每個列做內積 (行跟列都是詞向量)。
  投影的值越大 → 兩個向量相關度高

• 結果是 N×N 的矩陣，代表每個向量與其他向量的相似度（注意力分數）。

借用一下人家的圖，這裡可以看到"早"(每個向量)跟"上", "好" (其他向量) 做內積，得到右邊黃色的，也就是注意力分數，表示向量的相似度
  

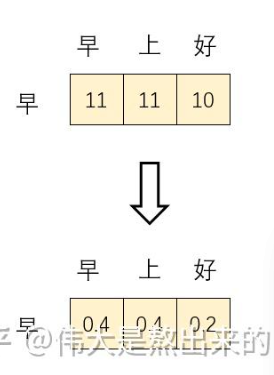
Softmax

• 對每一行進行 softmax，將注意力分數轉換成權重（機率分布介於0 ~ 1）。
  

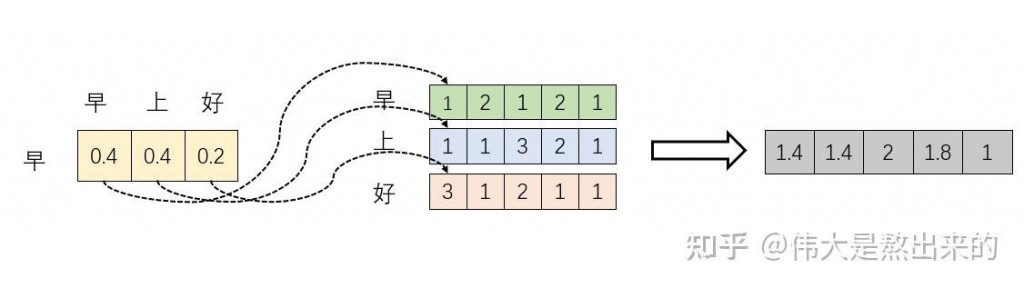
加權求和：Softmax(XX^T)X

• 將 softmax 出來的權重乘上原始的向量 X，最後總合(剛才複習提到的分子)。

經注意力機制加權求和得到的新向量。
  

今天主要講了比較多觀念，但還沒開始寫 code，可以先吸收吸收，今天就先到這囉~